哈希表是普通数组概念的推广,是能够根据关键码值(Key value)而直接进行访问的数据结构。也就是说,它通过把关键码值映射到表中一个位置来访问记录,以加快查找的速度。这个映射函数叫做散列函数(Hash Function),存放记录的数组叫做散列表(Hash Table)。
在平均情况下,在哈希表中查找一个元素的期望时间是 O(1)O(1) ,因此效率极高。Python中的字典就是采用了哈希表的结构。
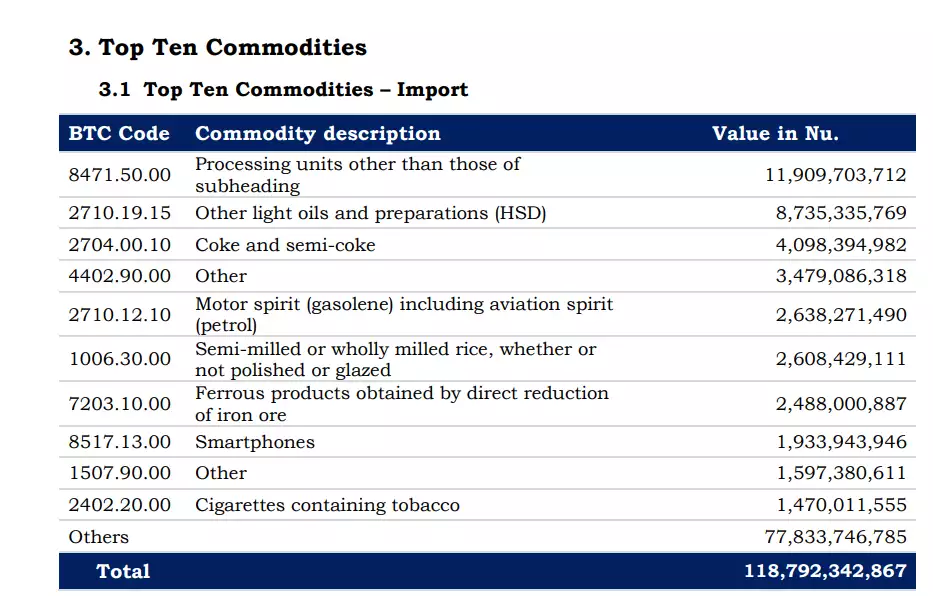
1. 直接寻址表
当关键字的全域 UU 比较小时,直接寻址简单有效,假设某应用要用到一个动态集合,其中每个元素都有一个取自于全域 U={0,1,..,m−1}U=\left\{ 0,1,..,m-1 \right\} 的关键字,且假设没有两个元素具有相同的关键字。
我们用数组(直接寻址表) T[0,...,m−1]T[0,...,m-1] 来表示该动态集合,其中每个位置对应全域 UU 中的一个关键字即可。
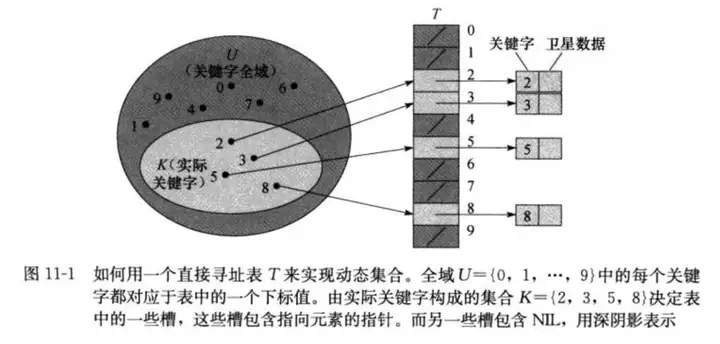
这样检索、插入和删除操作都是 O(1)O(1) 的时间。
但是如果全域 UU 很大,那么一台计算机的内容是无法存储的;如果实际要存储的关键字集合 K≪UK\ll U ,那么分配给 TT 的大部分空间都要浪费掉。因此我们产生了Hash Table
2. 哈希表
在直接寻址方式下,具有关键字 kk 的元素被存放在槽 kk 中,在散列方式下,利用散列函数 h(k)h(k) 根据关键字 kk 计算出槽的位置,函数 hh 将关键字全域 UU 映射到散列表 T[0,...,m−1]T[0,...,m-1] 的槽位上:
h:U→{0,...,m−1}h:U\rightarrow \left\{ 0,...,m-1 \right\}
这样就能够缩小需要处理的下标范围,即值域从 |U||U| 降到了 mm 。
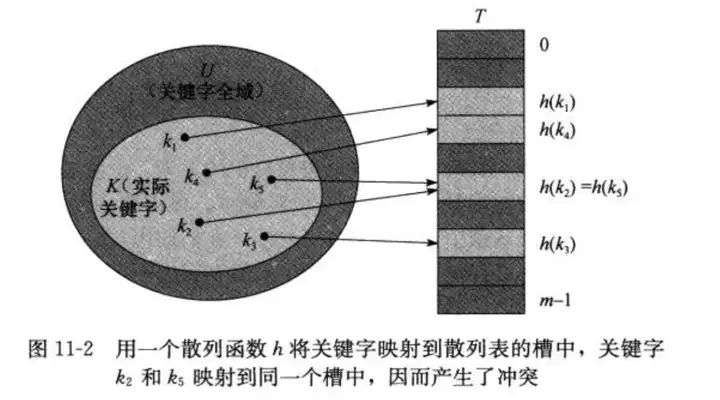
但这样存在一个问题,两个关键字可能映射到同一个槽上,称之为碰撞(collision)
,我们通过两种方法来进行解决。一个是链接法(chaining),另一个是开放寻址法(open addressing).
2.1 链接法(chaining)解决碰撞问题
在链接法中,把散列到同一槽中的所有元素放到一个链表中,槽 jj 中有一个指针,指向由所有散列到 jj 的元素构成的链表的头;如果不存在这样的元素,则置为NULL。
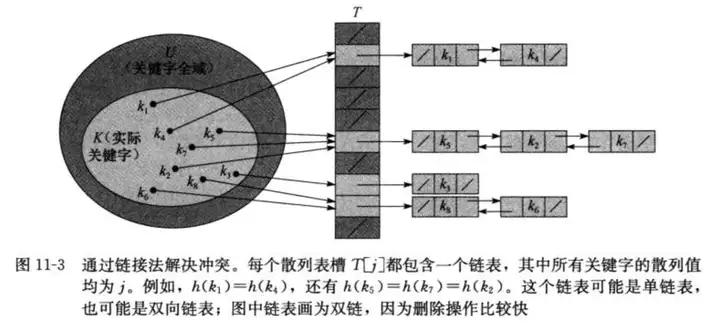
如果散列表中的槽树至少与表中的元素数成正比,即 n=O(m)n=O(m) ,则平均来说,查找操作需要常数量的时间;同时,插入操作在最坏情况下需要 O(1)O(1) 的时间,删除操作最坏情况下需要 O(1)O(1) 的时间,因此全部的字典操作平均情况下都可以在 O(1)O(1) 时间内完成。
其优点主要包括:
拉链法处理冲突简单,且无堆积现象,即非同义词决不会发生冲突,因此平均查找长度较短;在用拉链法构造的散列表中,删除结点的操作易于实现缺点:
在对链表进行存储空间分配的时候,会降低整个程序的运行速率,因为哈希冲突后,用链表去延展来解决。针对链表进行延展而效率低下的问题,出现了开放寻址法(Open addressing)。
2.2 开放寻址法(Open Addressing)解决碰撞问题
在开放寻址法中,所有的元素都存放在散列表中,因此哈希表的每个表项或包含一个元素,或包含NULL,而不像在链表法中,这里没有链表,也没有元素存放在散列表外。
在开放寻址法中,当要插入一个元素时,需要连续的检查(probe)散列表的各项,直到找到一个空槽来放置待插入的关键字为止,检查的顺序并非是 0,1,...,m−10,1,...,m-1 (这样查找时间为 Θ(n)\Theta(n) ),而是依赖于带插入的关键字,因此我们将散列表扩充为:
h:U×{0,...,m−1}→{0,...,m−1}h:U \times \left\{ 0,...,m-1 \right\} \rightarrow \left\{ 0,...,m-1 \right\}
对开放寻址法来说,要求对每一个关键字 kk ,probe序列为:
<h(k,0),h(k,1),h(k,2)...,h(k,m−1)><h(k,0),h(k,1),h(k,2)...,h(k,m-1)>
插入算法如下所示,即找到probe序列中第一个为空的表项插入。
查找算法与插入算法类似,在查找过程中,如果找到就返回;如果找到NULL,就查找失败。
在开放寻址中,删除操作执行较为困难,如果从槽 ii 中删除关键字,不能仅仅将表项置为NULL,这样的话,如果在插入某关键字 kk 的probe过程中,发现 ii 被占用了,则 kk 被插到后面的位置。当从槽 ii 中删除关键字后,则无法检索关键字 kk 。因此需要额外的机制,将删除的表项设置为DELETED,并且需要修改插入和查找算法。
但是如果使用了DELETED,查找时间就不再依赖于装载因子了,因此在必须删除关键字的应用中,往往采用链接法来解决碰撞。
常见的probe方法包括:
线性probe二次probe双重probe这里不做详细介绍。
3. 链接法哈希表代码实现
以下是采用链接法实现的哈希表,主要用了List来存放链表,并且为了提高检索速度实现了resize方法。